19  الأنواع

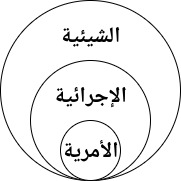
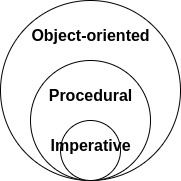
وقد عرفنا أن من طرائق البرمجة في بايثون:

• الأمرية (Imperative): تعليمات ينفذها البرنامج بتسلسل
• الإجرائية (Procedural): إجراءات تستدعي إجراءات بشكل هرمي
• والآن نعرف أنها أيضًا شيئية (Object-oriented): أشياء لها صفات وأفعال وتفاعلات مع أشياء أخرى قد تنتمي إلى نفس النوع

الطرائق البرمجية: الشيئية، الأمرية، الإجرائية

Programming Paradigms: Object-oriented, Procedural, Imperative

وقد كنا نتعامل مع أشياء طيلة هذه الفترة؛ بدءًا بالرقم (Number) ومرورًا بفروعه: (int) و (float) و (bool)، مرورًا بالقائمة (list) والصف (tuple) والنطاق (range) والنص (str)، وكذلك المجموعة (set) والقاموس (dict).

graph TD
    A[<b>شيء</b> <br> <code>Object</code>] --> B[<b>رقم</b> <br> <code>Number</code>]
    B --> E[<b>صحيح</b> <br> <code>int</code>]
    B --> F[<b>عشري</b> <br> <code>float</code>]
    B --> G[<b>مركب</b> <br> <code>Complex</code>]
    A --> D[<b>جمع</b> <br> <code>Collection</code>]
    D --> M[<b>تسلسل</b> <br> <code>Sequence</code>]
    M --> C[<b>نص</b> <br> <code>str</code>]
    M --> H[<b>قائمة</b> <br> <code>list</code>]
    M --> I[<b>صف</b> <br> <code>tuple</code>]
    M --> J[<b>نطاق</b> <br> <code>range</code>]
    D --> K[<b>مجموعة</b> <br> <code>set</code>]
    D --> L[<b>قاموس</b> <br> <code>dict</code>]

وكل الأنواع من نوع شيء (Object). ثم تتفرع الأنواع وتتفرع. وقد يدخل النوع في أكثر من نوع بحسب الاعتبار (يأتي تفصيله).

البرمجة الشيئية

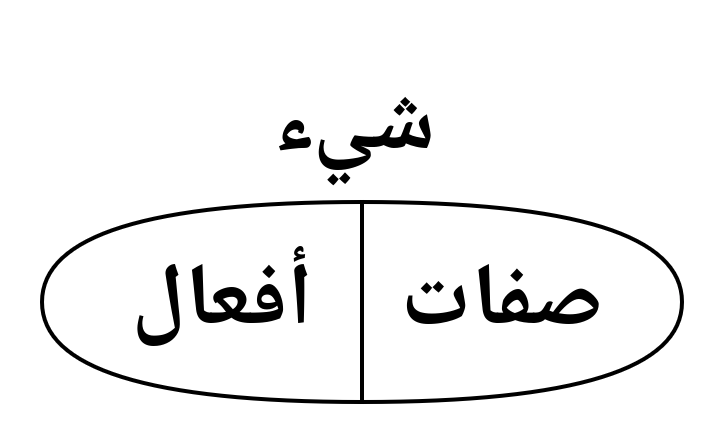
ففكرة البرمجة الشيئية تدور حول إسناد المتغيرات والإجراءات لشيء مُعَيَّنٍ من نوع ما. ونشبه هذه الأشياء بالمحسوسات فيقال أنها أشياء ذات صفات وأفعال؛ إشارةً إلى المتغيرات والإجراءات المسندة إليها. ومن هذه الأفعال ما يكون بين الأشياء؛ فهو تفاعل بين نوع ونوع.

الشيء

فمثلاً: نوع القائمة (list) يُنشأُ مِنهُ قائمة معيَّنة (هي الشيء: xs = [1, 2, 3]) يُسنَدُ إليها إجراءات الإضافة (xs.append) والحذف (xs.remove) والتعديل (xs[i] = x) ونحو ذلك.

وأما التفاعلات؛ فهي علي قسمين:

الأول: بين الشيء ونظيره (من نفس النوع)؛ وذلك نحو تعريف: list + list = list بحيث تعرَّف علامة + بين الشيئين بعملية الدمج (لا الجمع). وكان من الممكن أن تعرَّف بأنها جمع.

الثاني: بين الشيء وخلافه (من نوع آخر)؛ وذلك نحو: list.append(Any) فإن القائمة تقبل في فعل الإلحاق (append) أي نوع. ويمكن تقييد النوع الذي يقبله الفعل كما كنا نفعل في الإجراءات؛ إذْ الأفعال ما هي إلا إجراءات مُسندة إلى نوع.

تعريف النوع

الشيء: صفات وأفعال.

تأمل المثال التالي:

class Counter:
    def __init__(self, count):
        self.count = count
    
    def increment(self, by=1):
        self.count += by

• النوع (Class): Counter
• الصفات (Properties): فقط count
• الأفعال (Methods): increment

لاحظ:

• يتم إسناد المتغيرات للمعيَّن في فعل الإنشاء __init__
• تتقدَّم self (نفس) كعامل في الابتداء في جميع الأفعال؛ وهي تشير إلى الشيء المعيَّن (Instance) ؛ أي: أحد أفراد النوع.

إنشاء المعيَّنات

المعيَّن: أحد أفراد النوع.

ويسمى الفعل المخصوص __init__ بفعل الإنشاء (Initialization). وذلك أنه يتم تنفيذه عند استدعاء النوع هكذا:

c1 = Counter(10)

ونشير للصفة بعلامة النقطة: c1.count والفعل كذلك: c1.increment() على النحو التالي:

print(c1.count)
c1.increment(2)
c1.increment(3)
print(c1.count)

10
15

وهذا معيَّن آخر من نفس النوع:

c2 = Counter(0)

print(c1.count)
print(c2.count)

15
0

تغليف العمليات

التغليف (Encapsulation) آلية لإخفاء عمليات تفصيلية معقدة على البيانات المكنونة خلف إجراءات بسيطة.

فحينما عرفنا المتغير كصفة: count في الشيء Counter، أبرزنا من الإجراءات: increment فقط. وكأننا نقول: لا يمكن أن يعدِّل المستفيد على المتغير count إلا عن طريق الإجراء increment. وصحيح أنك تستطيع الوصول من الخارج إلى صفة المعيَّن: c1.count لتعديلها مباشرةً، إلا أن ذلك يخالف آلية التغليف.

في المثال التالي لا نريد للمستفيد أن يعدِّل على الرصيد balance إلا عن طريق الإجراء deposit الذي يضمن أمرين:

• قبليات (pre-conditions): كاشتراط أن الزيادة تكون موجبة قبل البدء
• بعديات (post-conditions): ضمان تسجيل تاريخ العملية بعد التمام

يتم ذلك في بايثون عن طريق جعل الصفة نفسها (balance) مخفيَّة، ونبدلها بصفة محميَّة: __balance بشرطتين سفليتين متقدِّمة. ثم نُبرِزُ الصفة عن طريق فعل قراءة؛ وذلك باستعمال المعدِّل @property، وهو يجعل الفعل balance يبرز كصفة بلا قوسين للاستدعاء balance() وذلك يعني أن مجرَّد عملية الوصول إلى الصفة (بعلامة النقطة: .) هو في الحقيقة استدعاء لفعل يعود بقيمة، لا بالصفة التي يمكن تعديلها.

class Account:
    def __init__(self, name, balance):
        self.name = name
        self.__balance = balance

    # الإيداع
    def deposit(self, amount):
        # قبليات الإيداع
        if amount <= 0:
            print("must be positive")
            return
        
        # الإيداع نفسه
        self.__balance += amount

        # بعديات الإيداع
        print('time of deposit:', '2027-07-07')

    @property
    def balance(self):
        return self.__balance

نقوم الآن بإنشاء هذا الشيء الذي يمثِّل حساب المستخدم (Account)، ثم نصِل إلى الصفة بعلامة النقطة: a1.balance؛ فيكون ذلك استدعاءً للإجراء الذي تم وضع المعدِّل @property عليه ليكون الوصول إليه كالصفة:

a1 = Account('Adam', 100)
a1.balance

100

ولو حاولت التغيير مباشرة على الصفة فإنك أصلاً لن تجد اسمها مُسندًا إلى الشيء:

a1.balance = 1000

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[26], line 1
----> 1 a1.balance = 1000

AttributeError: property 'balance' of 'Account' object has no setter

لكن يجوز فقط قراءة الصفة (قيمتها) لا التعديل عليها، هكذا (بعد الإيداع مثلاً):

a1.deposit(100)
a1.balance

time of deposit: 2027-07-07

200

وليظهر أثر الحماية، نجرِّب إيداع مبلغ سالب، ولاحظ رسالة الخطأ:

a1.deposit(-44)

must be positive

وهكذا نتصوَّر الشيء كأنه آلة مزوَّّدة بآليات عامَّة يسهل استعمالها في ظروف كثيرة بحيث تغير هذه الآليات من حالة الشيء في كل مرة ليؤدي وظائف معقَّدة لا تتم بسهول بمجرَّد إجراء ذو خطوات محددة دائمًا بتسلسل واحد.

العرض

نريد أن نعرِّف نوعًا جديدًا للإحداثيات (Point) ونريد أن نعرضها في جملة print بتمثيل يعبِّر عنها كإحداثيات.

يستعمل الفعل الخاص __repr__، ويعني التمثيل (Representation) لتخصيص طريقة عرض الشيء؛ سواءٌ إذا تم تمرير في print أو في آخر سطر من الخلية. كل ما عليك هو إعادة قيمة نصيَّة من ذلك الفعل.

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y
    
    def move(self, dx, dy):
        self.x += dx
        self.y += dy
    
    def __repr__(self):
        return f"Point({self.x}, {self.y})"

والآن إن عرفنا نقطة جديدة، ووضعناها على السطر لوحدها ، ستظهر لنا الإحداثيات، لا عنوانها في الذاكرة:

p = Point(3, 4)
p.move(7, 6)
p

Point(10, 10)

الإجراء الثابت

الإجراء الثابت: هو الإجراء المسند إلى النوع لا للمعيَّن.

فيمكن إسناد الإجراء للجنس لا للشيء الواحد، وذلك بإضافة المعدِّل @staticmethod عليه. ونمثل لذلك بإجراء حساب المسافة بين نقطتين: distance. ولاحظ عدم وجود self فيه:

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y
    
    def __repr__(self):
        return f"Point({self.x}, {self.y})"
    
    @staticmethod
    def distance(p1, p2, distance_type='euclidean'):
        if distance_type == 'euclidean':
            return ((p1.x - p2.x)**2 + (p1.y - p2.y)**2)**0.5
        elif distance_type == 'manhattan':
            return abs(p1.x - p2.x) + abs(p1.y - p2.y)

ثم يستعمل كأي إجراء، لكن بإسناده إلى النوع:

p1 = Point(3, 4)
p2 = Point(7, 6)
d = Point.distance(p1, p2, 'manhattan')
print('distance:', d)

distance: 6

المتغير الثابت

المتغير الثابت: هو المتغير المسند إلى النوع لا للمعيَّن.

يُسنَد المتغير للنوع بتعيينه بمحاذاة غيره من الإجراءات نحو ما فعلنا هنا بالمتغير decor. ولاحظ استعماله في الإجراء __repr__ في جملة if-else من غير استعمال self لأننا لا نشير إلى معيَّن.

class Point:
    decor = '<>'

    def __init__(self, x, y):
        self.x = x
        self.y = y
    
    def move(self, dx, dy):
        self.x += dx
        self.y += dy
    
    def __repr__(self):
        if Point.decor == '<>':
            return f"<{self.x}, {self.y}>"
        elif Point.decor == '[]':
            return f"[{self.x}, {self.y}]"
        else:
            return f"({self.x}, {self.y})"

فيمكن الآن تعديل المتغير decor للنوع:

p1 = Point(3, 4)
p2 = Point(7, 6)
print(p1, p2)

Point.decor = '[]'
print(p1, p2)

<3, 4> <7, 6>
[3, 4] [7, 6]

هيكل البيانات

تختلف كفاءة استرجاع البيانات وكتابتها والتعديل عليها بحسب شكل هذه البيانات في الذاكرة وشكلها على جهاز التخزين فعليًّا. وهذا ما نسميه بهيكلة البيانات (Data Structure). ومن أمثلة ذلك:

• المصفوفة (Array)
• الشجرة (Tree)
• الرسم (Graph)

وغيرها كثير. وسنمثل على ذلك بتشكيل الكومة في بايثون:

الكومة (Stack)

نريد أن نعرِّف نوعًا من هياكل البيانات يسمى الكومة (Stack)، وكأنه يمثِّل مجموعة مكدسة من الأوراق؛ إذ له فعلين:

• وضع ورقة: push(item) وكأنك تضع ورقة فوق الأوراق السابقة
• سحب ورقة: pop() وكأنك تسحب ورقةً من الأعلى
• لمحة سريعة: peek() وكأنك تنظر إلى الورقة العليا دون سحبها

وأقرب شيء له في بايثون هو القائمة (list) ولذلك ستكون هي تمثيلها الداخلي.

class Stack:
    def __init__(self):
        self.items = []

    def push(self, item):
        self.items.append(item)
    
    def pop(self):
        return self.items.pop()
    
    def peek(self):
        return self.items[-1]

    def __repr__(self):
        return f"|{'|'.join(str(item) for item in self.items)}>"

• فعل الإنشاء يُسنِد قائمة فارغة إلى الشيء (self)
• فعل push يضيف إلى آخر هذه القائمة بالفعل append
• فعل pop يأخذ آخر عنصر من القائمة بالفعل pop (وهو إزالة مع أخذ)
• فعل __repr__ يعطينا تمثيلاً للكومة بالاعتماد على تمثيل القائمة

نجرب الآن أن ننشئها ثم نضع أربعة عناصر فيها ونظهرها:

s = Stack()
s.push(10)
s.push(20)
s.push(30)
s.push(400)
print(s)

|10|20|30|400>

والآن نسحب عنصرًا (من الأخير)، ونظهرها:

s.pop()
print(s)

|10|20|30>

ويمكن النظر في العنصر الأعلى دون سحبه بالفعل peek:

print(s.peek())

30