2  توالي الأوامر

يُرى التدفق (Flow) المستمر في النظام الميكانيكي للسيارة ليبقيها سائرة بفعل الوقود. كما يُرى في حركة الطاحونة المائية حيث يدفعها جريان النهر فيحركها معه. ويُرى أيضًا في شراع السفينة حيث تضرب فيه الرياح. والكهرباء مثلها تيار يسري في أنبوبة المصباح ليبقيه منيرًا، أو في نظام التكييف ليبقي الجو باردًا.

وأصل المنطق الرقمي (Digital Logic) تيارات كهربائية لها تردد ينبض بسرعة فائقة لما تلتقطه عين الإنسان. فإذا نظرت للإشارة علمت أننا تحكمنا في سرعة هذا التردد بحيث تصبح ألوان الإشارة تتبدل وتنطفئ وتُشعَل بتوقيتٍ مضبوط. لكنها مع ذلك ليسَت خوارزميَّة. لأنها أشبَهُ بالكُرة التي تُدفعُ من أعلى مُنحَدَرٍ فتتدحرجُ بفعل الجاذبية. إذْ تعملُ الإشارة بوتيرة معلومة وتدور وتدور مادامت الكهرباء تنبض فيها.

ولا يكاد يخلو برنامج مفيد من اتخاذ قرارات مغايرة بناءً على اختلاف الظروف المكانية والزمانية والواقعية. فلو كان نظام التحكُّم في التقاطُع المروري يراعي حركة السيْر بحيث يُقدِّم ويؤخِّر في توقيت فتح إشاراته لتحقيق أعلى كم من العبور للسيارات؛ فإننا نسميها إشارة ذكيَّة (Smart). وهذه خوارزمية.

ومن أمثلة ذلك:

• مراعاة المكان: جعل السيارة الآلية تتقيَّد بالسرعة القانونية للشارع الذي هي فيه
• مراعاة الزمان: توقيت إيقاف المكيِّف حتى تستيقظ في الصباح الباكر
• مراعاة الواقع: إضاءة المصباح عند استشعار حساس الحركة بدخول شخصٍ إلى الغرفة

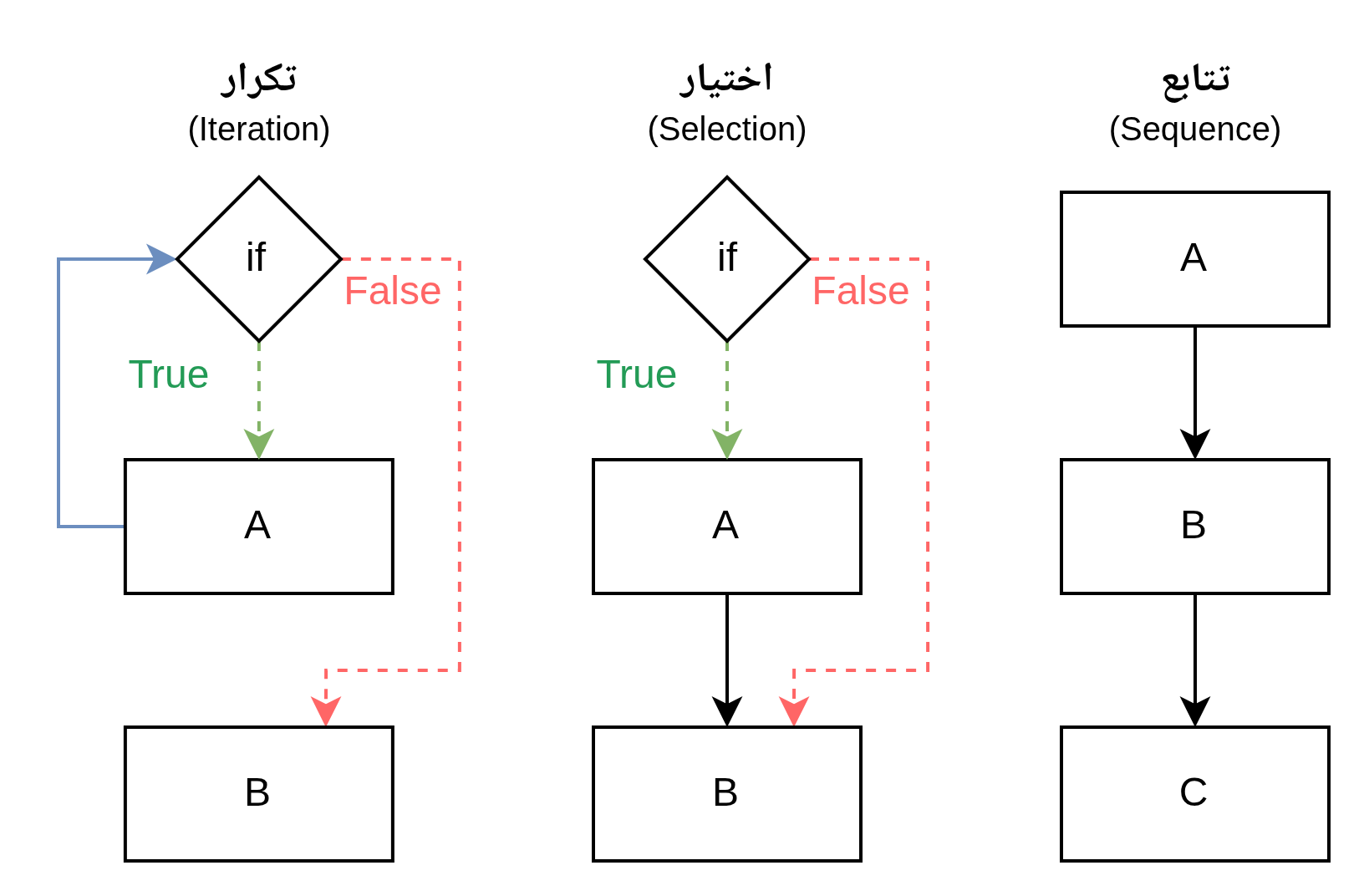
ويتم ذلك بأوامر التحكم في سير الأوامر (Control-flow) وهي جُمَل شرطيَّة ينبني عليها اختيار الأمر التالي. فإن الأوامِر في المنطق الرقمي تنتظم في ثلاثة صوَر:

1. تتابع (Sequence): وهو الأصل؛ حيث يكون الانتقال من الأمر إلى الأمر الذي يليه مباشرة
2. اختيار (Selection): حيث يكون الانتقال مشروطًا (لاحظ في الصورة أن تنفيذ A مشروط)
3. تكرار (Iteration): وهو نوعٌ من الاختيار، يكون فيه الانتقال إلى الوراء؛ ويتم لنا بذلك الإعادة

أنماط توالي الأوامر

وإذا استُعمِلَت هذه لتحقيق غاية محددة بعدد محدود من الخطوات، صار اسمها خوارزمية (Algorithm).

فإن جملة التعيين التالية تكتُب قيمة 20 في نفس المحلّ الذي كتبت عليه جملة التعيين الأولى 10. لذا ظهرت النتيجة: 20.

flowchart TD
    A[x = 10] --> B[x = 20] --> C["print(x)"]

x = 10
x = 20
print(x)

20

القيمة المنطقية

ويتم اختيار أحد طريقين في سيْر الأوامِر بحسب ناتج تعبير منطقي (bool)؛ وهي أحد اثنين:

1. نعم: True؛ ويقال أيضًا: صحيح أو مطابق أو ثابت
2. لا: False؛ ويقال أيضًا خاطئ أو مخالف أو منتفي

ومن العبارات المنطقية في بايثون، حاصل عوامل المقارنة كما في المثال:

a = 10
b = 5

print(a == b)   # يساوي
print(a != b)   # لا يساوي
print(a > b)    # أكبر من
print(a < b)    # أصغر من 
print(a >= b)   # أكبر من أو يساوي
print(a <= b)   # أصغر من أو يساوي

False
True
True
False
True
False

تذكر: أن لكل قيمة نوعًا. فإذا وضعت المتغير في دالة type(x) لمعرفة النوع، فإنك ستعرف أن مثل هذه التعبيرات نوعها منطقي (bool). مثال:

print(type(8 == 5))

<class 'bool'>

ويمكن المقارنة بين النصوص كذلك، ونتيجة ذلك قيمة من النوع المنطقي أيضًا؛ لأن المقارنة تعبير منطقي:

print("Hello" == "Hello") # يجب أن تتطابق جميع الحروف
print("a" == "A")         # حالة الحرف مهمة

True
False

ولاحظ أن النص والعدد -لاختلاف نوعيهما- يكون حاصل المساواة بينهما لا (False):

print(10 == "10")

False

لكن بايثون تتجوَّز في المساواة بين الأنواع المختلفة التي من صنف العدد، فالمطابقة بين العدد الصحيح (int) وذي الفاصلة العائمة (float) جائزة في بايثون:

print(10 == 10.0)

True

التخيير

يتم التخيير المذكور آنفًا بالجملة الشرطية:

if <boolean expression>:
    <code>

• فتبدأ الجملة الشرطية بكلمة if (إذا) ويليها التعبير المنطقي (كما سبق بيانه)
  • فيكون ما يندرج تحتها (بالمسافة) الأوامر المتعلقة بنفاذ الشرط (True). فإن انتفى الشرط (False) فإن بايثون تتخطى هذه الأوامر وتقفز لما بعدها.

وبالمثال يتضح المقال:

flowchart TD
    IF{{if cond}} -- False --> X["Outside"]
    IF -- True --> Y["Inside"] --> X["Outside"]

  style IF fill:#82aeff, stroke:#333, stroke-width:2px;
  linkStyle 0 color:red;

cond = False
if cond:
    print('Inside')
print('Outside')

Outside

لاحظ أن الشرط منتفٍ، لذلك كان حاصل النص السابق تخطي ما بداخل الجملة الشرطية، وطباعة Outside فقط.

تنبيه: محاذاة المسافات

لاحظ أن المسافة البادئة (Indentation) (أي: المسافات من بداية السطر حتى يُدرج الكلام أسفل كلمة if) في القطعة البرمجية أعلاه ليست لمجرد تسهيل القراءة، بل تُفسَّرُ الجُملةُ أنها في الداخل أو الخارج بناءً على وجودها وعدمها. فهي التي تضع الحدود حول المشروط. ويجب أن تكون محاذية فإذا كان مقدارها 4 مسافات أو 2 أو أكثر، فوجب أن تكون جميع الجُمَل بنفس المقدار. وهذا ما نسميه المحاذاة.

لاحظ: أن خلو الشرط من جُمَل مشروطة به يُفرِز تنبيهًا للمبرمج عند تفسير النص البرمجي:

flowchart TD
    IF{{if True}}
    Y["Inside"] --> X["Outside"]
    style IF fill:#fc0000, stroke:#333, stroke-width:2px;

if True:
print('Inside')
print('Outside')

  Cell In[8], line 2
    print('Inside')
    ^
IndentationError: expected an indented block after 'if' statement on line 1

إذا قمت بزيادة المحاذاة لكل من جملتي print()، فسوف يعمل النص البرمجي بتدفِّقٍ غيرِ الذي قصدناه ابتداءً. أي أنه سيطبع Outside عندما يكون في الواقع داخل اللَّبِنَة الشرطية.

flowchart TD
    IF{{if True}}
    IF -- True --> Y["Inside"] --> X["Outside"]
    
    style IF fill:#82aeff, stroke:#333, stroke-width:2px;

if True:
    print('Inside')
    print('Outside')

Inside
Outside

يؤدي النص البرمجي السابق إلى خطأ منطقي (لا نحوي) لن يظهر أبدًا كخطأ ولن يوقف البرنامج!

ملاحظة

لا تنسَ أن المحاذاة في بايثون هي أساسية لتفسير النص البرمجي.

التخيير الحصري

لجعل التخيير بين أمرين بحيث لو حصل أحدهما لا يحصل الآخر، فإننا نتبع الشرط الأوَّل بكلمة وإلا (else)، على النحو التالي:

if <boolean expression>:
    <code_1>
else:
    <code_2>

مثلاً، تريد أن تظهر رسالة خطأ لو لم تطابق كلمة المرور:

input_password = hash("abc123")
stored_password = hash("fuda$(#*(lm")

is_match = input_password == stored_password

if is_match:
    msg = "Welcome"
else:
    msg = "Try Again"

print(msg)

Try Again

وهذه الشجرة توضح تسلسل التنفيذ الإجرائي لها:

flowchart TD
    IF{{if is_match}}
    IF -- False --> D["msg = 'Try Again'"]
    IF -- True --> C["msg = 'Welcome'"]
    D --> E["print(msg)"]
    C --> E["print(msg)"]

    style IF fill:#82aeff, stroke:#333;
    linkStyle 0 color:red;

ولاحظ أن print(msg) غير مشروطة، لذلك فإنها مع نفوذ الشرط أو عدمه يتم تنفيذها.

الجبر المنطقي

والنوع الثنائي (bool) الذي ينحصر في قيمتين فقط هو أصل المنطق الرقمي المعروف بالأصفار والآحاد. حيث نشأ علم الجبر المنطقي (Algebraic Logic) من قبل عالم الرياضيات جورج بول الذي وضع أسسه في كتابه: “قوانين الفكر” (The Laws of Thought) في عام 1854.

ملاحظة

ومن بديع صنع الله سبحانه وتعالى، أن هذه العمليات الثلاثة بها تتكون جميع المعالجات التي تصير في كل جهاز حاسب بلا استثناء!

وإذا كان جبر الأعداد يكون بالمعادلات التي هي مقابلات تمثل قيَم عددية، وبينها عوامل الجمع والضرب والقسمة والطرح والأس ونحو ذلك؛ فإن الجبر المنطقي يكون بمعادلات تمثل مقابلات لقيم منطقية (صفر أو واحد)، بينها العوامل الأساسية الثلاثة التالية (ويمثل الصفر المنطقي بكلمة False والواحد المنطقي بكلمة True):

العامل الأول: العكس (not). مثاله:

a = 10 > 5  # تعيين لحاصل تعبير منطقي للمتغير
b = not a   # عكس القيمة المنطقية التي في المتغير الأول
print(b)    # طباعة

False

العامل الثاني: الجمع (and). مثاله:

a = True
b = False
print(a and b)

False

العامل الثالث: الخيار (or). مثاله:

a = True
b = False
print(a or b)

True

وقد وضعت الجمع والخيار في جدولٍ واحد فيه جميع الاحتمالات بينهما ليسهل استيعابه:

a	b	a and b	a or b
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	1

مآل العبارات المنطقية في الجملة الشرطية

على سبيل المثال:

age = 20
weight = 50

if age > 18 and weight > 45:
  print("You are eligible to donate blood")

You are eligible to donate blood

يؤول طرفا العامل and لقيمة منطقية هكذا:

• age > 18 تؤول إلى True لأن age=20 وهو أكبر من 18
• weight > 45 تؤول إلى True لأن weight=50 وهو أكبر من 45
• فتكون الجملة إذًا: True and True وهي تؤول إلى True

وهذه الشجرة تمثل تسلسل تفسير العبارات المنطقية في الجملة الشرطية، لتؤول إلى نعم أو لا (True أو False):

graph BT
  RESULT((if))
  ROOT{and} -- True --> RESULT
  middle_left{">"} -- True --> ROOT
  middle_right{">"} -- True --> ROOT
  left_left[age] -- "20" --> middle_left
  left_right[18] -- "18" --> middle_left
  right_left[weight] -- "50" --> middle_right
  right_right[45] -- "45" --> middle_right

تستعمل الأقواس (()) لتجميع الشروط لإيقاع الترتيب المنطقي المراد:

age = 16
temperature = 15
is_wearing_coat = True

if age < 16 or (temperature < 20 and not is_wearing_coat):
  print("I suggest you don't go outside")

• age < 16 تؤول إلى False لأن age=16 ليست أصغر من 16
• temperature < 20 تؤول إلى True لأن temperature=15 أصغر من 20 فعلاً
• not is_wearing_coat تؤول إلى False لأن is_wearing_coat=True وهي عكسها
• إذًا الجملة بين القوسين (temperature < 20 and not is_wearing_coat) تؤول إلى True and False وهي تؤول إلى False
• إذًا الجملة age < 16 or (False) تؤول إلى False or False وهي تؤول إلى False

وهذه الشجرة تمثل تسلسل تفسير العبارات المنطقية في الجملة الشرطية:

graph BT
  RESULT((if))
  ROOT{or} -- False --> RESULT
  middle_left{"<"} -- False --> ROOT
  middle_right{and} -- False --> ROOT
  left_left[age] -- "16" --> middle_left
  left_right[16] -- "16" --> middle_left
  right_middle{"<"} -- True --> middle_right
  right_not{not} -- False --> middle_right
  right_temp[temperature] -- "15" --> right_middle
  right_val[20] -- "20" --> right_middle
  right_coat[is_wearing_coat] -- True --> right_not

تسمية العبارات المنطقية

ويجوز تسمية العباراة المنطقية وتعيين قيمتها لمتغيرات لبيان موقعها في سياق الجملة الشرطية:

is_minor = age < 16
is_cold = temperature < 20

if is_minor or (is_cold and not is_wearing_coat):
  print("I suggest you don't go outside")

ومن فوائد تعيين العبارة المنطقية لمتغير: إمكانية استعماله في أكثر من موضع.

تسلسل المقارنات

وتفهم بايثون المقارنات المتسلسلة. فعبارة x < y <= z تكافئ x < y and y <= z:

low = 10
high = 20
x = 15

(low < x < high) == (low < x and x < high)

True

الجملة الشرطية المتكاملة

الصيغة المتكاملة للجملة الشرطية:

if <boolean expression>:
    <code_1>
elif <boolean expression>:
    <code_2>
elif <boolean expression>:
    <code_3>
else:
    <code_4>

• أما جملة إذا (if) فقد سبق بيانها
• وأما جملة وإلا فإن (elif) فلا يتم تنفيذها إلا عند تخلُّف الشرط السابق لها. وقد تتعدد (كما في المثال)
• وأما جملة وإلا الأخيرة (else) فلا يتم تنفيذها إلا عند تخلف جميع الشروط السابقة لها.

ونؤكد أن الجمل الشرطية اللاحقة بعد إذا (if) الأولى؛ كل واحدة منها مرتبطة بانتفاء ما قبلها. وهذا ما يوضحه الرسم الشجري التالي:

flowchart TD
    IF1{{if}}
    IF1 -- False --> ELIF1{{elif}}
    IF1 -- True --> code_1
    ELIF1 -- False --> ELIF2{{elif}}
    ELIF1 -- True --> code_2
    ELIF2 -- False --> ELSE{{else}}
    ELIF2 -- True --> code_3
    ELSE --> code_4

    style IF1 fill:#82aeff, stroke:#333, stroke-width:2px;
    style ELIF1 fill:#82aeff, stroke:#333, stroke-width:2px;
    style ELIF2 fill:#82aeff, stroke:#333, stroke-width:2px;
    style ELSE fill:#82aeff, stroke:#333, stroke-width:2px;
    linkStyle 0,2,4 color:red;

جرب

استكشف المنطق التالي بتغيير قيمة x كل مرة للتبع ما يحصل في كل مرة:

• x = -5
• x = 0
• x = 1
• x = 5

x = -5

if x < 0:
    x = 0
    print('Set to zero')
elif x == 0:
    print('Zero')
elif x == 1:
    print('Single')
else:
    print('More')

print("Always:", x)

Set to zero
Always: 0

وهذه الشجرة توضح تسلسل التنفيذ الإجرائي لها:

flowchart TD
    IF{{if x < 0}}
    IF -- False --> ELIF{{elif x == 0}}
    IF -- True --> S1[x = 0] --> S2["Set to zero"]
    ELIF -- False --> ELSE{{else}}
    ELIF -- True --> S3[x = 1] --> S4["Single"]
    ELSE --> S5["More"]

    Always[Always: x]
    S2 --> Always
    S4 --> Always
    S5 --> Always

    style IF fill:#82aeff, stroke:#333, stroke-width:2px;
    style ELIF fill:#82aeff, stroke:#333, stroke-width:2px;
    style ELSE fill:#82aeff, stroke:#333, stroke-width:2px;
    linkStyle 0,3 color:red;

وهذا تصوير لسير الإجراءات لنفس النص البرمجي. ملاحظة: اضغط على الزر Prev أو Next للتنقل بين خطوات التنفيذ الإجراءية:

لاحظ أن العبارة الأخيرة خارج كل اللَّبِنات الشرطية لذا يتم تنفيذها دائمًا.

للمزيد تابع الملحق بالجملة الشرطية المتكاملة.