3  الدالة

والدالة (Function) قطعة نص برمجيّ لها اسم. وتسمى أيضًا الإجراء (Procedure). وهي من أقوى المركبات البرمجية التي تتم بها الخوارزميات.

خذ على سبيل المثال وحدة الرياضيات (math) التي يتم الاستفادة منها بعد جملة الاستيراد (import) على النحو التالي:

import math

فالعالم بالرياضيات برمج هذه الدوال وأعطاها اسما، فنستطيع استعمالها في حل المسائل الرياضية:

print(math.sqrt(16))  # الجذر التربيعي
print(math.pow(2, 3)) # القوة
print(math.cos(math.radians(45))) # جيب الزاوية 45 درجة

4.0
8.0
0.7071067811865476

ولولا مفهوم تخزين الأوامر وتسميتها، للزم أن نكتب الأوامر البرمجية التي تؤدي هذه الحسابات في كل مرة نريدها. وهذا يتعذر علينا لا لأنها خطوات كثيرة فحسب بل لأنها ليست بسيطة بحيث يتقنها كل مبرمج أصلاً.

وقد تحتوي الوحدات على مسميات، كالثابت \(\pi\) الذي يستعمل في علم المثلثات:

print(math.pi)

3.141592653589793

تسمى النقطة (.) عامل إسناد (Dot Operator) في نحو العبارة math.pi أو عبارة math.sin(A)؛ وتفسرها بايثون أنها إشارة للمسمى المتضمن في الوحدة المسنَد إليها. سواءٌ كان ذلك دالة أو متغيرًا.

ويجدر بالذكر أن بعض الدوال في لغة بايثون لا نحتاج فيها لإسنادها لوحدةٍ ما؛ فهي مبنيَّة (Built-in)، نحو: print()، بل ولا تحتاج إلى التصريح باستيرادها بجملة (import). ومثال ذلك أيضًا round() لتقريب العدد. ولم يتبيَّن لي وجه الفرق بين ما جُعِلَ مبنيًّا في وحدة أو مبنيًّا عائمًا.

print(round(math.pi, 4))

3.1416

ويُمكن إشاعة المسميات المتضمَّنة في وِحدةٍ ما بجملة الاستيراد المبتدأة بمِن (from) بحيث لا نحتاج لإسنادها في كل مرة، وذلك يتم هذا النحو:

from math import sin, radians

c = 1000
A = 40
B = 60
C = 80

a = c * sin(radians(A)) / sin(radians(C))
h = a * sin(radians(B))
print(h)

565.2579374235679

ويُمكِن استيراد الكُلّ بعلامة النجمة (*)، على هذا النحو:

from math import *

z = cos(2*pi) - sin(pi/2)
print(z)

0.0

تنبيه: استيراد الكل (*) قد يتعارض مع مسمياتنا فيما بعد، ويصعب أن نعرف ذلك بسهولة، لذلك يجب أن يستعمل بحذر!

والمكتبة (Library) اسمٌ يطلق على مجموعة الوحدات.

وللاطلاع على الوحدات المدمجة (Built-in Modules) في لغة بايثون، يمكن الرجوع إلى صفحات بايثون المرجعية للمكتبة الأساسية (Standard Library) https://docs.python.org/3/library. حيث تجد -مثلاً-:

• وحدة الإحصاء: https://docs.python.org/3/library/statistics.html
• وحدة العشوائية: https://docs.python.org/3/library/random.html
• وحدة الوقت والتاريخ: https://docs.python.org/3/library/datetime.html

وهذه كلها يمكن استيرادها ثم استعمالها لأنها من ضمن بايثون نفسها، فلا تحتاج إلى تنزيل وتثبيت.

إنشاء دالة

أسباب إنشاء الإجراء:

• التكرار: إذا وجدت أنك تكرر نفس القطعة البرمجية مرارًا
• التعقيد: إذا كانت العملية تحتاج لكد الذهن أو لمعرفة لا تتوفر عند الجميع
• القابلية للتركيب: إذا كانت القطعة ككل ذات وظيفة واضحة ومحددة، ورأيت أنها تنسجم مع غيرها من القطع إذا وضعت لها اسمًا

ونمثل بتعريف الإجراء هذا:

def calculate_bmi(weight, height):
    sq = height ** 2
    bmi = weight / sq
    return round(bmi, 2)

ويبتدأ تعريفه بكلمة def (تعني: Define)، ويليها اسمه، ويليه بين القوسين: معطياته: (weight, height). ويلي ذلك علامة الابتداء (:)، ونسرد بعدها جسده؛ وهي الأوامِر التي تعالج هذه المعطيات. ويختص الإجراء بجملة الرجوع (return x) التي تعود بالنتيجة x للمكان الذي استُدعيَ منه الإجراء.

ثم يحصل الاستدعاء (Call) بذكر اسم الإجراء مع عامل الاستدعاء (Call Operator) وهما القوسان بعده () وهما كالظرف تُمَرر إليه المعطيات فيهما.

result = calculate_bmi(70, 1.80)
print(result)

21.6

تعيين معطيات الإجراء بالاسم

ويجوز تعيين المعطى بالاسم لا بالموضع:

result = calculate_bmi(height=1.80, weight=70)
print(result)

21.6

ولاحظ أننا قلبنا الترتيب لنبين أنه ليس بلازمٍ إذا تمَّ التعيين بالاسم.

المعرفات في الإجراء لا تتسرب إلى الخارج

ومن خصائص الإجراء أن أي اسم يتم تعريفه داخل الإجراء فإنه معروفٌ في نطاقه وليس يتسرب العلم به إلى الخارج.

فنتوقع وقوع خطأ هنا لأن bmi غير معرَّفة في الخارج:

print(bmi)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[10], line 1
----> 1 print(bmi)

NameError: name 'bmi' is not defined

تقول رسالة الخطأ (السطر الأخير) أن المتغير bmi غير معرَّف. وهذا منطقي لأن النطاق الخارجي لا يعلم ما تكنه النطاقات الداخلية الخاصة بالإجراءات. وهو أمر مطلوب جدًّا ومرغوب في البرمجة. وذلك يعني أننا لن نتعب كثيرًا في اختيار الأسماء داخل كل إجراء، مخافة التعارض.

دالة: قوة كلمة المرور

وإليك مثالاً آخر لدالة تتحقق من قوة كلمة المرور:

def check_password_stength(password):
    if len(password) < 8:
        return "Weak"
    elif len(password) < 12:
        return "Medium"
    else:
        return "Strong"

لاحظ أننا استعملنا الدالة المبنية len() لحساب عدد الأحرف في النص.

ثم نستعمل دالتنا:

print(check_password_stength("1234"))
print(check_password_stength("1234567890"))
print(check_password_stength("12345678901234567890"))

Weak
Medium
Strong

دالة: حساب المسافة المستقيمة بين نقطتين

في هذا المثال نعرف نقطتين ثم نحسب المسافة بينهما. والمسافة الإقليدية بين نقطتين \((x_1, y_1)\) و \((x_2, y_2)\) تتبع معادلة فيثاغورس:

\[ \text{distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]

ونكتبها في بايثون هكذا كدالة:

import math

def distance(x1, y1, x2, y2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

ثم نستعملها:

print(distance(0, 0, 3, 4))
print(distance(x1=1, y1=1, x2=-2, y2=-2)) # أو بتعيين المعطيات بالاسم

5.0
4.242640687119285

الإجراء المتسلسل

الإجراء المتسلسل (Recursive Function): هو إجراء يطلب نفسه؛ بشكل مباشر أو غير مباشر. وحتى يكون مثمرًا: يجب أن تؤول سلسلة الطلبات هذه إلى جملة تُنهي التسلسل.

مثال: المضروب

فمثلا: تعرف الرياضيات مضروب العدد

\[ !n = n(n-1)(n-2)\cdots(1) \]

فهي عملية ضرب لكل عدد مع الذي قبله حتى ينتهي للواحد. ونمثل هنا لمضروب العدد 5:

\[ !5 = (5)(4)(3)(2)(1) = 120 \]

ولك أن تصف نفس العملية هكذا:

\[ !n = n !(n-1) \]

أي أن مضروب العدد هو ضربُ هذا العدد في مضروب العدد الذي قبله. وذلك يتسلسل على النحو التالي:

\[ \begin{align*} !5 &= (5)!(4) \\ &= (5)(4!(3)) \\ &= (5)(4(3!(2))) \\ &= (5)(4(3(2!(1)))) \\ &= (5)(4(3(2(1)))) \\ &= (5)(4)(3)(2)(1) \\ &= 120 \end{align*} \]

إذاً نعرِّف المعادلة في بايثون هكذا:

def factorial(n):
    # Recursive case (تسلسل)
    if n > 0:
        recursive_result = factorial(n - 1)
        return n * recursive_result
    # Terminal case (نهاية)
    return 1

factorial(5)

120

حيث لدينا حالتان:

• عندما تكون n > 0 يتم الطلب الذاتي : recursive_result = factorial(n - 1) إذْ هي جملة متسلسلة تكدِّس طلبات فوق طلبات؛ لكنها تؤول في النهاية إلى الجملة التي تُنهي التسلسل
• return 1 هي الجملة التي تنهي التسلسل

وهنا قطعة نص برمجي نستعملها لتصور تسلسل الطلبات:

def factorial(n, depth=0):

    # Recursive case (تسلسل)
    print(f"{'  ' * depth}Call factorial({n})")
    if n > 0:
        result = n * factorial(n - 1, depth + 1)
        print(f"{'  ' * depth}Return {result} from factorial({n})")
        return result
    
    # Terminal case (نهاية)
    print(f"{'  ' * depth}Return 1 from factorial({n})")
    return 1

factorial(5)

Call factorial(5)
  Call factorial(4)
    Call factorial(3)
      Call factorial(2)
        Call factorial(1)
          Call factorial(0)
          Return 1 from factorial(0)
        Return 1 from factorial(1)
      Return 2 from factorial(2)
    Return 6 from factorial(3)
  Return 24 from factorial(4)
Return 120 from factorial(5)

120

• فكل طلب يُنشأ له ظرف تنفيذ جديد تكون بالنسبة له قيمة n هي المعيَّنة له وقت النداء.
• وهكذا يتم تكديس الطلبات حتى ينتهي التسلسل عند الطلب factorial(0) الذي يؤول لنتيجة مباشرة: return 1 فيخلَّى هذا الظرف من الذاكرة وتعود نتيجته إلى الظرف المباشر الذي استدعاه وهو ظرف factorial(1).
• فتتعين القيمة recursive_result = 1 وينتقل إلى الجملة التي بعدها وهي جملة الرجوع بنتيجة return n * recursive_result وهُما معيَّنان، أي تكون الجملة في واقع الظرف: return 1 * 1.
• وهذه النتيجة تعود للظرف الذي استدعاه وهو factorial(2) … إلخ.

طلب الإجراء المتسلسل يؤدي إلى ظروف متداخلة تؤول إلى ظرف واحد في النهاية.

يستعمل الإجراء المتسلسل وكذلك هياكل البيانات المتسلسلة بشكل كبير في الخوارزميات الفعالة.

يسهل كتابة بعض الخوارزميات باستعمال الإجراء المتسلسل. لكن قد تكون (أحياًنا) أقل أداءً من استعمال الحلقات.

صورة البرنامج كسلسلة استدعاءات متراكمة

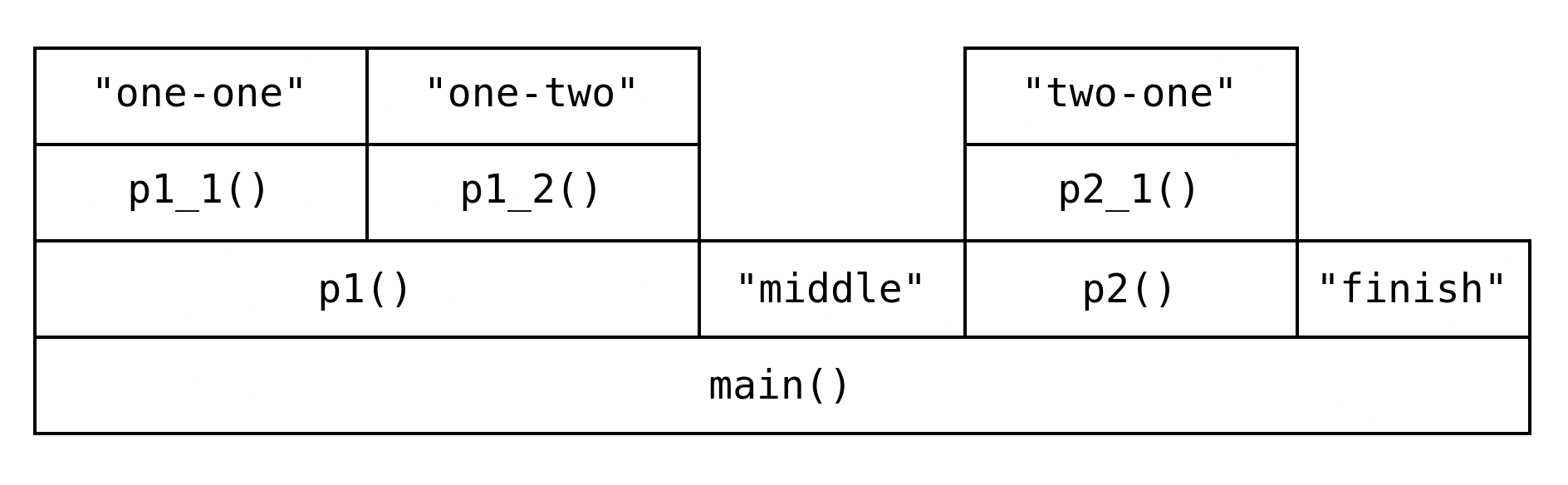
غالبًا ما تفكك المهمة الكبيرة إلى خطوات جزئية على شكل إجراءات منفصلة، ويتم استدعاؤها وربط نتائجها في الإجراء الأوَّل (main()). لذلك نتصوَّر أن البرنامج عبارة عن سلسلة من الاستدعاءات، التي قد تتضمن في طيها استدعاءات أخرى فتتراكم.

def main():
    p1()
    print("middle")
    p2()
    print("finish")

def p1():
    p1_1()
    p1_2()

def p2():
    p2_1()


def p1_1():
    print("one-one")

def p1_2():
    print("one-two")


def p2_1():
    print("two-one")

main()

one-one
one-two
middle
two-one
finish

لاحظ أننا نصوِّر كومة الاستدعاءات (Call Stack) بمرور الوقت من اليسار إلى اليمين، بحيث كلما ازداد عرض الطبقة كان ذلك دليلاً على قضاء وقت أكثر في تنفيذ تلك الجزئية، مما يساعدنا في معرفة الأجزاء التي تحتاج لتسريع في البرنامج حتى يكون في المحصلة سريعاً.

كومة استدعاءات البرنامج السابق

ملاحظة

توجد مكتبة خارجية لعرض كومة الاستدعاءات حقيقة وهي: SnakeViz وهي تتطلب معرفة بـ cprofile. ويُعرف ذلك بالرسم اللهبي (Flamegraph).

فأي إجراء يتم تعريفه؛ كالمتغير الذي يتم تعريفه: هو نص برمجي محفوظ ينتظر الاستدعاء حتى يحضر في ذاكرة البرنامج في ظرف تنفيذي ويتم تشغيله بعوامل معيَّنة. ثم يعود إلى الإجراء الذي استدعاه، وهكذا دواليك. لذا فإننا إن لم نشغيل الإجراء الأوَّل main فإن البرنامج وإن كان يحفظ هذه الإجراءات إلا أنها تحتاج إلى الاستدعاء لتعمل.

للمزيد راجع ملحق الدالة.