day1 = 10
day2 = 15
day3 = 30
day4 = 20
day5 = 25
day6 = 0
day7 = 54 التسلسل
لنفترض أننا نريد حساب مجموع عدد صفحات القراءة خلال الأسبوع. فنجعل لكل يوم متغيرًا تحفظ فيه عدد الصفحات التي قرأناها في ذلك اليوم.
ثم نريد جمع ذلك كله، لمعرفة مجموع الصفحات خلال الأسبوع
total = day1 + day2 + day3 + day4 + day5 + day6 + day7
print(total)105ونريد أن نعرف المعدَّل اليومي، وذلك بقسمة المجموع على عدد الأيام:
mean = total / 7
print(mean)15.0فهنا تبيَّن لنا أمران:
- تكرار كتابة اسم المتغير سبعة مرات
- تكرار كتابة العملية التي بينها ستة مرات
- القسمة على عدد ثابت (
7) لأننا نعرف أن عددها سبعة
حسنًا لو أردنا أن نعرف المعدل اليومي خلال الشهر؟ ماذا لو قلنا خلال السنة؟ الأمر سيطول كثيرًا.
وهذا النمط في البرمجة هو: عرض مجموع بيانات على إجراء واحدة تلو الأخرى من أولها إلى آخرها. وتعبر بايثون عن القائمة (list) التي هي سلسلة بيانات، بالقوسين المربعين [] على النحو التالي:
days = [10, 15, 30, 20, 25, 0, 5]- وقد وضعت بايثون للجمع إجراء
sum(list) - ولمعرفة عدد العناصر إجراء
len(list)
فنوظفهما لمقصدنا كالتالي:
total = sum(days)
mean = total / len(days)
print(total)
print(mean)105
15.0حسنًا ماذا لو أردنا تعريف الدالة sum(list) والدالة len(list) بأنفسنا؟ فكيف ستبدوا؟
التعيين النسبي
وجب علينا أولاً أن نرجع إلى جملة التعيين (Assignment) التي عرفناها في الفصل الأوَّل. تذكر أن علامة = هي جملة تعيين وليست مساواةً كما في الرياضيات. فالتعيين اللاحق ناسخٌ لأي تعيين يسبقه.
x = 10
x = 20
print(x)20ولك أيضًا أن تستعملها لزيادة المتغير أو إنقاصه، وهو ما يسمى التعيين النسبي:
x = 100
x = x + 100
x = x - 50
x = x * 2
x = x / 4
print(x)75.0ولنفهم ذلك نتصوَّر أن المتغير في الطرف الأيمَن يتم التعويض عنه بقيمته، ثم يتم حساب العمليَّة (100 + 100) ثم يتم التعيين فتنتقل النتيجة من الطرف الأمين إلى x في الطرف الأيسر. فأصبحت قيمة x بعد السطر الثاني: 200.
ثم سطر الطرح: ننظر أوَّلاً للطرف الأيمن فنعوِّض المتغير x بقيمتها 200 ثم نُجري العملية: (200 - 50) ثم يتم تعيين حاصل ذلك بموجب علامة التعيين = للطرف الأيسر: x. فتصبح قيمة x بعد السطر الثالث: 150.
وقل مثل ذلك في الضرب والقسمة.
وتعبِّر بايثون للتعين النسبي (Augmented Assignment) باختصار هكذا:
x = 100
x += 100
x -= 50
x *= 2
x /= 4
print(x)75.0الكر
نعود إلى مسألتنا وهي تعريف إجراء يحسب مجموع الأعداد. لمعرفة كيفية ذلك؛ فإن بايثون تعبِّر عن آليَّة العبور على العناصر بجملة الكر (Iteration) وتبدأ بكلمة for وذلك على النحو التالي (وسنجعلها في إجراء):
def sum2(numbers):
total = 0
for x in numbers:
total += x
return totalلاحظ أننا استعملنا اسمًا لا يتعارض مع الاسم الموجود. والمتغير total في هذا السياق يسمى المُراكِم (Accumulator) إذْ يُستعمَل لتحصيل القيمة النهائية خطوة بعد خطوة. وأما جملة الكر (for x in numbers) فإنها تمرُّ على عناصر المجموعة numbers، فتقرأ أول واحدٍ فيها فتسميه x ثم تنفذ ما وضعنا في جسدها. ثم تأخذ الثاني فتفعل مثل ذلك. ثم تأخذ الثالث فتفعل مثل ذلك. وهلم جرا .. حتى تمر على آخر عنصر. وأما جملة الرجوع return total فهي التي ترجع بقيمة المتغير الذي فيه النتيجة.
ثم نستعمل هذا الإجراء:
z = sum2(days)
print(z)105وأما إجراء العد len() فعلى هذا النحو:
def len2(numbers):
count = 0
for _ in numbers:
count += 1
return countولاحظ أننا وضعنا _ بدلاً من x لأنه لا تهمنا قيمة أي عنصر في المجموعة. فهدفنا مجرد العد من الأول إلى الأخير.
ونستعمل هذا الإجراء:
y = len2(days)
print(y)7والآن نستطيع أن نركب هذين الإجرائين لمعرفة المعدَّل، وسنعرف إجراءً له:
def mean(numbers):
return sum2(numbers) / len2(numbers)ونستعمل هذا الإجراء:
m = mean(days)
print(m)15.0الإشارة
إننا بالتعبير بالقوسين المربعين [] اختصرنا كثيرًا من التكرار في الكتابة. لكن لو سئلت كيف تقرأ قيمة اليوم الأخير؟ أو كيف تقرأ قيمة اليوم الأوَّل؟ فقد كان الجواب عن ذلك باستعمال اسم المتغير: day1 و day7 على النحو التالي:
print(day1)
print(day7)10
5وهذا يمكن التعبير عنه بعامل الإشارة [i]، حيث تكون الإشارة نسبةً إلى بداية التسلسل. فالعنصر الأوَّل هو [0] والعنصر الثاني هو [1] وهلمَّ جرا. فتقول:
print(days[0])
print(days[6])10
5وتستطيع أن تعرف اليوم الأخير، بعد العناصر بالإجراء len() ثم تطرح منه 1 وتجعل النتيجة في عامل الإشارة [i] كالتالي:
i = len(days) - 1
print(days[i])5وحتى لا يطول ذلك، فإن بايثون تعبر عنه باختصار بالإشارة بالسالب هكذا [-1] كالتالي:
print(days[-1])5قائمة طويلة
وتخيل أن هذه البيانات استمرَّت شهرًا فيه أربعة أسابيع، هكذا:
days = [
10, 15, 10, 30, 40, 20, 8,
30, 20, 15, 50, 30, 5, 10,
5, 45, 20, 10, 5, 40, 30,
7, 15, 10, 30, 40, 20, 9,
]وأما جعلها في أربعة أسطر، فإنه من قبيل الترتيب، ولا يؤثر في معناها بالنسبة لبايثون. فلو أردت عددها فسترى أنها \(7 \times 4 = 28\) عنصرًا:
print(len(days))28وكذلك الأول والثاني والثالث، والأخير والذي قبله والذي قبله:
print(days[0])
print(days[1])
print(days[2])
print(days[-1])
print(days[-2])
print(days[-3])10
15
10
9
20
40والأوسَط:
mid = len(days) // 2
print(days[mid])5إجراء الحساب على بعض القائمة
هب أننا نريد أن نحسب مجموع ما قرأناه في آخر يومين من كل أسبوع. ونريد أن نعرف في كل كرة موضعنا من التسلسل حتى نعرف هل نحن في وسط الأسبوع أم في آخره.
تزودنا بايثون بدالة النطاق range(start, stop, step) وبالاستعمال تتضح:
for i in range(0, 10, 2):
print(i)0
2
4
6
8وهذه معناها:
- البداية هي
0 - النهاية هي
10 - الخطوة هي
2
وهذا يعني أننا نبدأ من 0 ونصل إلى 10 بخطوة مقدارها 2، فنحصل على الأعداد: 0, 2, 4, 6, 8. ولاحظ أن النهاية غير مشمولة.
وإذا مررنا معطيين، فإنهما يفسرنا على أنهما البداية والنهاية، والقيمة الافتراضية للخطوة هي 1:
for i in range(1, 10):
print(i)1
2
3
4
5
6
7
8
9وإذا كان المعطى واحدًا؛ فإنه يفسَّر بأنه النهاية، والقيمة الافتراضية للبداية هي 0:
for i in range(10):
print(i)0
1
2
3
4
5
6
7
8
9والآن نستعمل النطاق لتوليد الأرقام بحيث تكون النهاية هي عدد الأيام، فيحصل لنا هذا الكر:
for i in range(len(days)):
print(i)0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27- فأما نهاية الأسبوع الأوَّل فهي
5و6 - وأما نهاية الأسبوع الثاني فهي
12و13 - وأما نهاية الأسبوع الثالث فهي
19و20 - وأما نهاية الأسبوع الرابع فهي
26و27
فنستطيع أن نقول:
total = 0
for i in range(len(days)):
if i == 5 or i == 6 or i == 12 or i == 13 or i == 19 or i == 20 or i == 26 or i == 27:
total += days[i]
print(total)142وهذه الطريقة طويلة. وتوجد طريقة أفضل من هذه باستعمال الحسابات المقاسية.
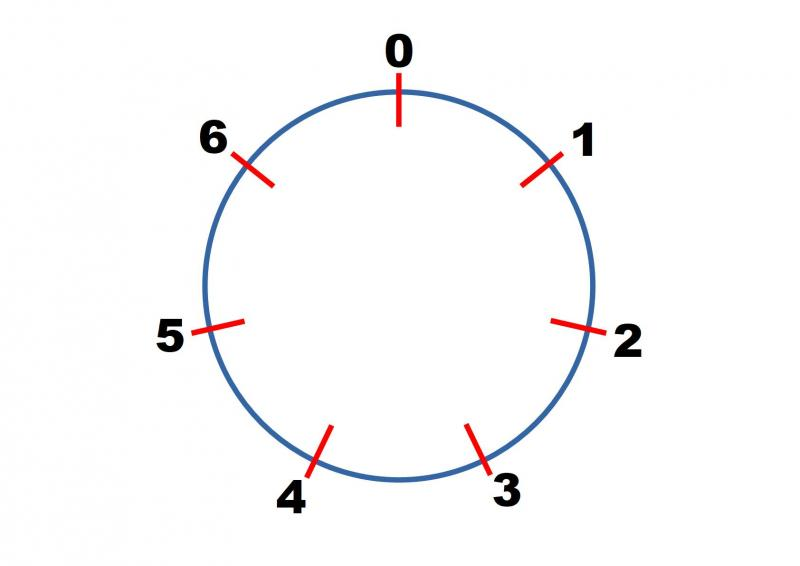
الحسابيات المقاسية (Modular Arithmetic) تتحرك فيه الأرقام بالجمع والضرب ونحوه بحيث تلتف الأرقام حول بعضها البعض عند الوصول إلى قيمة معينة، تسمى القياس (Modulus).
وهذه العملية التي تراها في الصورة، نعبر عنها في بايثون بباقي القسمة % من حاصل زيادة المدة إلى الساعة:
(9 + 4) % 121وها نحن نعود إلى المسألة الأصلية ونستعمل باقي القسمة بحيث تكون الدوْرة سبعة أيام للأسبوع، فتصير الأرقام بعد 4 هما فقط 5 و 6 ثم ترجع إلى 0 وهكذا تدور:
total = 0
for i in range(len(days)):
if i % 7 > 4:
total += days[i]
print(total)142الشريحة
وإذا أردنا حساب مجموع الأسابيع على حدة، فإننا نحتاج لاستخراج العناصر السبعة الأولى فقط. وهذا يحصل بعامل الإشارة وتمرير قيمة شريحة (slice ويعبر عنها بالنطقتين الرأسيتين :)، وذلك على هذا النحو:
week1 = days[0:7]
print(week1)[10, 15, 10, 30, 40, 20, 8]ولاحظ أن النهاية لا تشمل العنصر رقم 7 وإنما غايتها العنصر رقم 6.
وإذا كانت البداية من 0 فكتابتها وعدمه واحدة:
week1 = days[:7]
print(week1)[10, 15, 10, 30, 40, 20, 8]وكذلك الأسبوع الثاني والثالث والرابع:
week2 = days[7:14]
week3 = days[14:21]
week4 = days[21:28]
print(week1, '-->', sum(week1))
print(week2, '-->', sum(week2))
print(week3, '-->', sum(week3))
print(week4, '-->', sum(week4))[10, 15, 10, 30, 40, 20, 8] --> 133
[30, 20, 15, 50, 30, 5, 10] --> 160
[5, 45, 20, 10, 5, 40, 30] --> 155
[7, 15, 10, 30, 40, 20, 9] --> 131فإذا كانت القائمة فيها عدة أشهر، فإن هذا أيضًا سيطول. ويمكننا هنا أن نستعمل النطاق لتوليد الأرقام بسبع خطوات بينها، واستعمال الشريحة من الخطوة التي نكون فيها سبعًا إلى الأمام. وذلك على النحو التالي:
for i in range(0, len(days), 7):
print(sum(days[i:i+7]))133
160
155
131فإذا أردت لكل أن تحسب مجموع القراءة بين اليومين الأخيرين لكل أسبوع على حدة فهكذا:
for i in range(0, len(days), 7):
print(sum(days[i+5:i+7]))28
15
70
29الجدول: السلاسل المتقابلة
ومن أنماط المجموعات: القوائم المرتبطة عناصرها ببعض. وهي الجداول (Tables).
افترض أن لديك قائمة بالمصروفات (expenses) والإيرادات (revenues) لكل رُبع من السنة، وتريد حساب صافي الربح (net) لكل ربع على حدة، ثم جمعها لتحصل على الربح الإجمالي للسنة.
revenues = [52000, 51000, 48000, 50000]
expenses = [46800, 45900, 43200, 47000]
net = [ 0, 0, 0, 0]فإننا نستعمل نفس الرقم (i) للإشارة هنا وهنا أثناء الكر، حتى نجري الحساب على القيَم المتقابلة، ونضع ناتج ذلك في موضعٍ يقابلهما في سلسلة ثالثة (net)، وذلك على النحو التالي:
for i in range(len(revenues)):
net[i] = revenues[i] - expenses[i]
print('quarterly net:', net)
print(' annual net:', sum(net))quarterly net: [5200, 5100, 4800, 3000]
annual net: 18100ولاحظ أن جملة التعيين net[i] = ... تحلُّ محلَّ الصفر الذي كان فيه.
التصفية
وقد تكون بيانات المصروفات والإيرادات مسجَّلة في سلسلة واحدة بالقيَم الموجبة والسالبة. ونريد فصلها لمجموعتين، لنحسب متوسط هذه ومتوسط هذه على حدة. وهذا النمط يتكرر كثيرًا وهو التصفية (Filtering): وهي استخراج العناصر بحسب معيارٍ.
تصور أن لدينا قائمة من الأرقام الموجبة والسالبة في مجموعة واحدة، ونريد فصلها لمجموعتين:
transactions = [1200, -500, 300, -200, 450, -1000, 800]تقبل المجموعة إضافة العنصر إليها بالإجراء .append() المُسنَد إليها:
revenues = []
expenses = []
for x in transactions:
if x >= 0:
revenues.append(x)
else:
expenses.append(x)
print('average revenues:', sum(revenues) / len(revenues))
print('average expenses:', sum(expenses) / len(expenses))average revenues: 687.5
average expenses: -566.6666666666666الأكبر والأصغر
فإذا أردت معرفةَ أكبرها وأصغرها، فقد تستعمل الدالتين: max() و min()، على النحو التالي:
print(min(revenues), max(revenues))
print(min(expenses), max(expenses))300 1200
-1000 -200الترتيب
وإذا أردت عرضها مرتبةً من الأصغر إلى الأكبر، فتستعمل دالَّة الترتيب sorted()، على النحو التالي:
print(' sorted:', sorted(revenues))
print('unsorted:', revenues) sorted: [300, 450, 800, 1200]
unsorted: [1200, 300, 450, 800]وإذا أردتها بالعكس، فتغير المُعطى (reverse) من قيمته الإفتراضيَّة False إلى القيمة True، على النحو التالي:
print(' sorted:', sorted(revenues, reverse=True))
print('unsorted:', revenues) sorted: [1200, 800, 450, 300]
unsorted: [1200, 300, 450, 800]للمزيد راجع ملحق القائمة.